CC3 for NEXAFS spectra

Experimental [1] and simulated oxygen K-edge NEXAFS spectrum of acrolein. The simulated stick spectra are broadened with Lorentzian functions with a FWHM of 0.2 eV. The CCSD spectrum is shifted by -1.97 eV to match the most intense peak of the CC3 spectrum. The CC3 and CCSD spectra are shifted by +0.38 eV to account for relativistic effects.

For the simulation of core level spectroscopy the inclusion of triples is crucial to describe the contraction of the electron density when exciting a core electron. Due to the unfavorable scaling of CCSDT, CC3 has been implemented in eT [2] including EOM transition moments. The implemented algorithm is currently the most efficient one for EOM CC3 properties making it possible to treat systems of more than 500 basis functions.

References:
[1] D. Duflot, J. P. Flament, I. C. Walker, J. Heinesch, and M. J. Hubin-Franskin, "Core shell excitation of 2-propenal (acrolein) at the O1s and C1s edges: An experimental and ab initio study", J. Chem. Phys. 118(3)(2003)
[2] A. C. Paul, R. H. Myhre, and H. Koch, "A new and efficient implementation of CC3", J. Chem. Theory Comput. 17(1) (2021) https://doi.org/10.1021/acs.jctc.0c00686

Multilevel Hartree-Fock theory

Active MLHF density of a subregion of a gramicidin dimer [1].

In the study of large systems the property of interest can be localized in a specific subspace - e.g. in the case of molecules in a solvent or chromophores in protein structures. Different levels of theory can then be applied to regions that require different accuracy. In MLHF [2] the full space density is split into an active density, which is optimized through a density-based SCF procedure, and an inactive density, which only contributes to the optimization through its two-electron terms in the Fock operator. The wave function obtained with this procedure can be used as reference for a CC calculation on the active region or a subspace of the active region, to target localized properties.

References:
[1] S. D. Folkestad, E. F. Kjønstad, R. H. Myhre, J. H. Andersen, A. Balbi, S. Coriani, T. Giovannini, L. Goletto, T. S. Haugland, A. Hutcheson, I-M. Høyvik, T. Moitra, A. C. Paul, M. Scavino, A. S. Skeidsvoll, Å. H. Tveten, and H. Koch, "eT 1.0: An open source electronic structure program with emphasis on coupled cluster and multilevel methods", J. Chem. Phys. 152(18) (2020), https://doi.org/10.1063/5.0004713
[2] S. Sæther, T. Kjærgaard, H. Koch, and I-M Høyvik, "Density-Based Multilevel Hartree-Fock Model", J. Chem. Theor. Comput. 13(11) (2017)

The QM/Fluctuating Charge (QM/FQ) approach

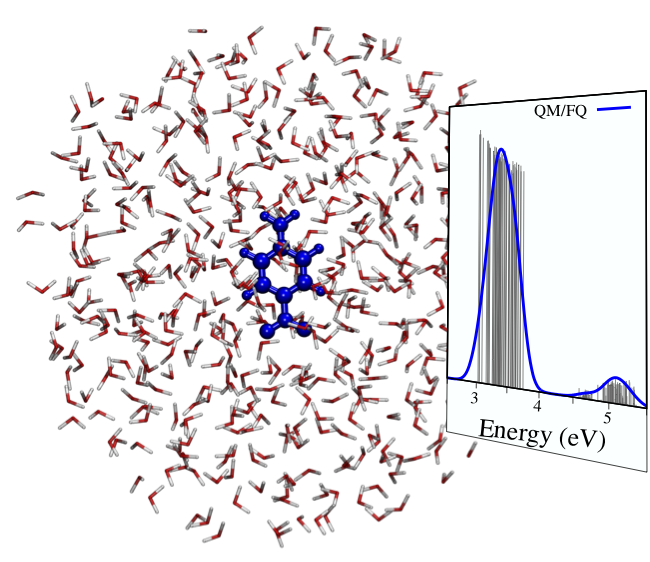
The UV/Vis spectrum of p-nitroaniline in aqueous solution calculated at the CC2/aug-cc-pVDZ QM/FQ level, as the average of 64 snapshots extracted from a classical Molecular Dynamics (MD) simulation [1].

The eT software can also perform QM/Molecular Mechanics (MM) calculations, using electrostatic and polarizable embeddings. In particular, in QM/MM the studied system is partitioned in a fragment, which is treated at high level of theory, whereas the embedding is described by means of classical force fields. In electrostatic embedding, each MM atom is endowed with a fixed charge, and the QM and MM portions interact by classical electrostatics. Mutual polarization between the two parts is recovered in polarizable embedding. In eT software, the polarizable QM/Fluctuating Charge (FQ) is implemented, which is particularly tailored to aqueous solution [2].

References:
[1] S. D. Folkestad, E. F. Kjønstad, R. H. Myhre, J. H. Andersen, A. Balbi, S. Coriani, T. Giovannini, L. Goletto, T. S. Haugland, A. Hutcheson, I-M. Høyvik, T. Moitra, A. C. Paul, M. Scavino, A. S. Skeidsvoll, Å. H. Tveten, and H. Koch, "eT 1.0: An open source electronic structure program with emphasis on coupled cluster and multilevel methods", J. Chem. Phys. 152(18) (2020), https://doi.org/10.1063/5.0004713
[2] T. Giovannini, F. Egidi, and C. Cappelli, "Molecular spectroscopy of aqueous solutions: a theoretical perspective", Chem. Soc. Rev. 49(16) (2020)

Time-dependent coupled cluster theory

Time-dependent one-electron density of a UV-pumped LiF molecule, shown as the difference from the stationary ground state density in the xz-plane. The time delay is with respect to the peak of the UV pulse. Molecular geometry and pump polarization are given in Ref. [1].

The time-dependent coupled cluster code [1] can be used to model molecular interactions with a user specified set of external laser pulses. The interaction is treated semiclassically, using the dipole approximation and length gauge. Time-dependent dipole moment and electric field vectors can be calculated and Fourier transformed using the code. The time-dependent one-electron density can also be calculated and evaluated on a 3D grid, and thereafter be visualized using e.g. Chimera.

References:
[1] A. S. Skeidsvoll, A. Balbi, and H. Koch, "Time-dependent coupled-cluster theory for ultrafast transient-absorption spectroscopy", Phys. Rev. A 102(2) (2020), https://doi.org/10.1103/PhysRevA.102.023115

Multilevel coupled cluster theory for NEXAFS spectra

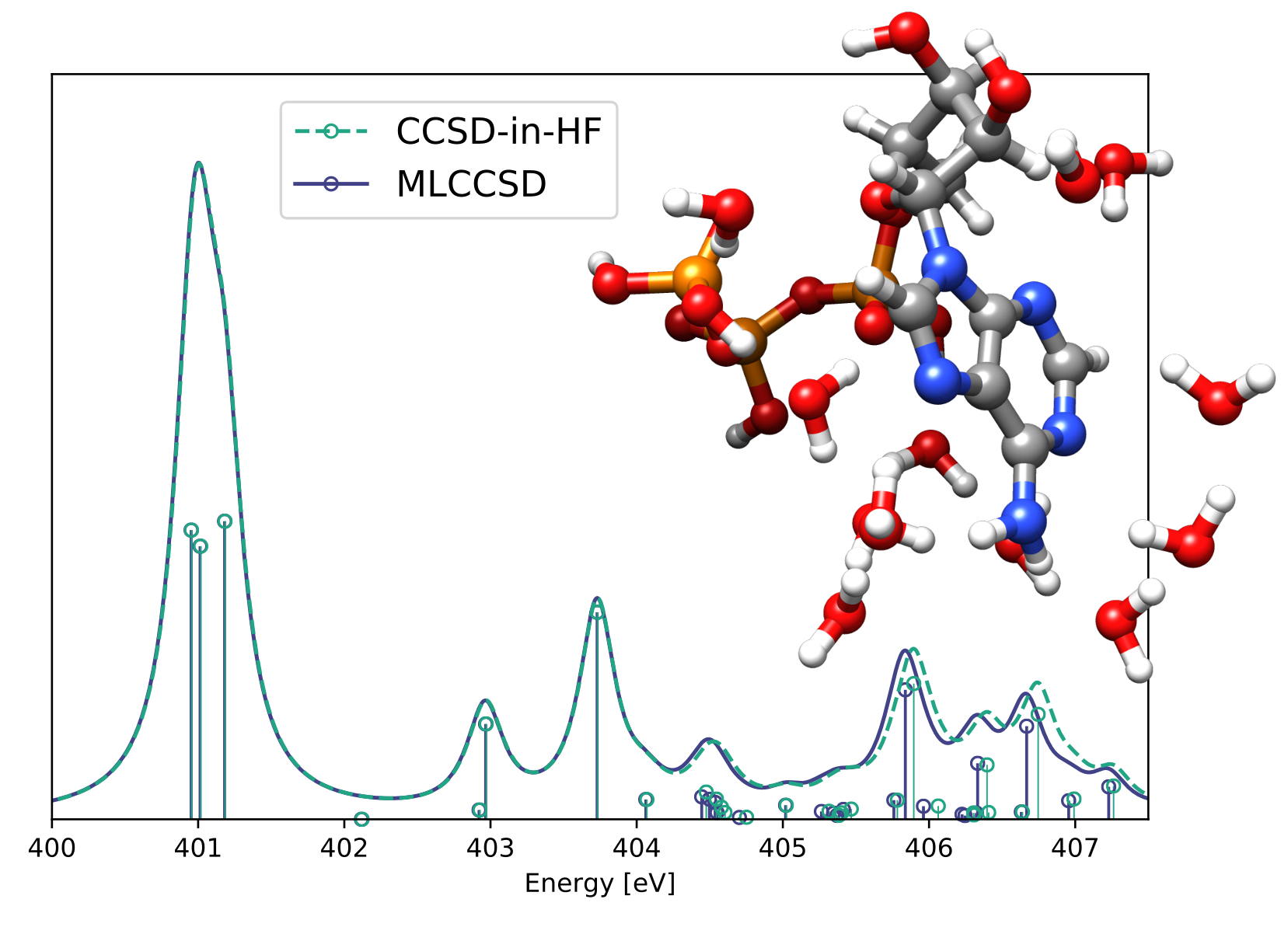
Multilevel coupled cluster singles and doubles (MLCCSD) and reduced space CCSD calculations (CCSD-in-HF) of the nitrogen K-edge spectrum of adenosine-triphosphate (ATP) with 12 water molecules [1]. The active space is selected by constructing a set of localized orbitals on the adenine-part of ATP.

The multilevel coupled cluster approach can be used to approximate coupled cluster excitation energies and transition strengths. The MLCCSD and MLCC2 models [2] are implemented in eT and can be used for valence and core excitation processes. The models are especially suited for core excitations and excitations on a target molecule in a solvent. For excitations located in a subregion of the molecule, the reduced space CC-in-HF models can be used to approximate the coupled cluster or multilevel coupled cluster excitation energies.

References:
[1] S. D. Folkestad and H. Koch, "Equation-of-motion MLCCSD and CCSD-in-HF oscillator strengths and their application to core excitations", J. Chem. Theory Comput. 16(11) (2020), https://doi.org/10.1021/acs.jctc.0c00707
[2] S. D. Folkestad and H. Koch, "Multilevel CC2 and CCSD Methods with Correlated Natural Transition Orbitals", J. Chem. Theory Comput. 16(1) (2020), https://doi.org/10.1021/acs.jctc.9b00701

Similarity constrained coupled cluster theory

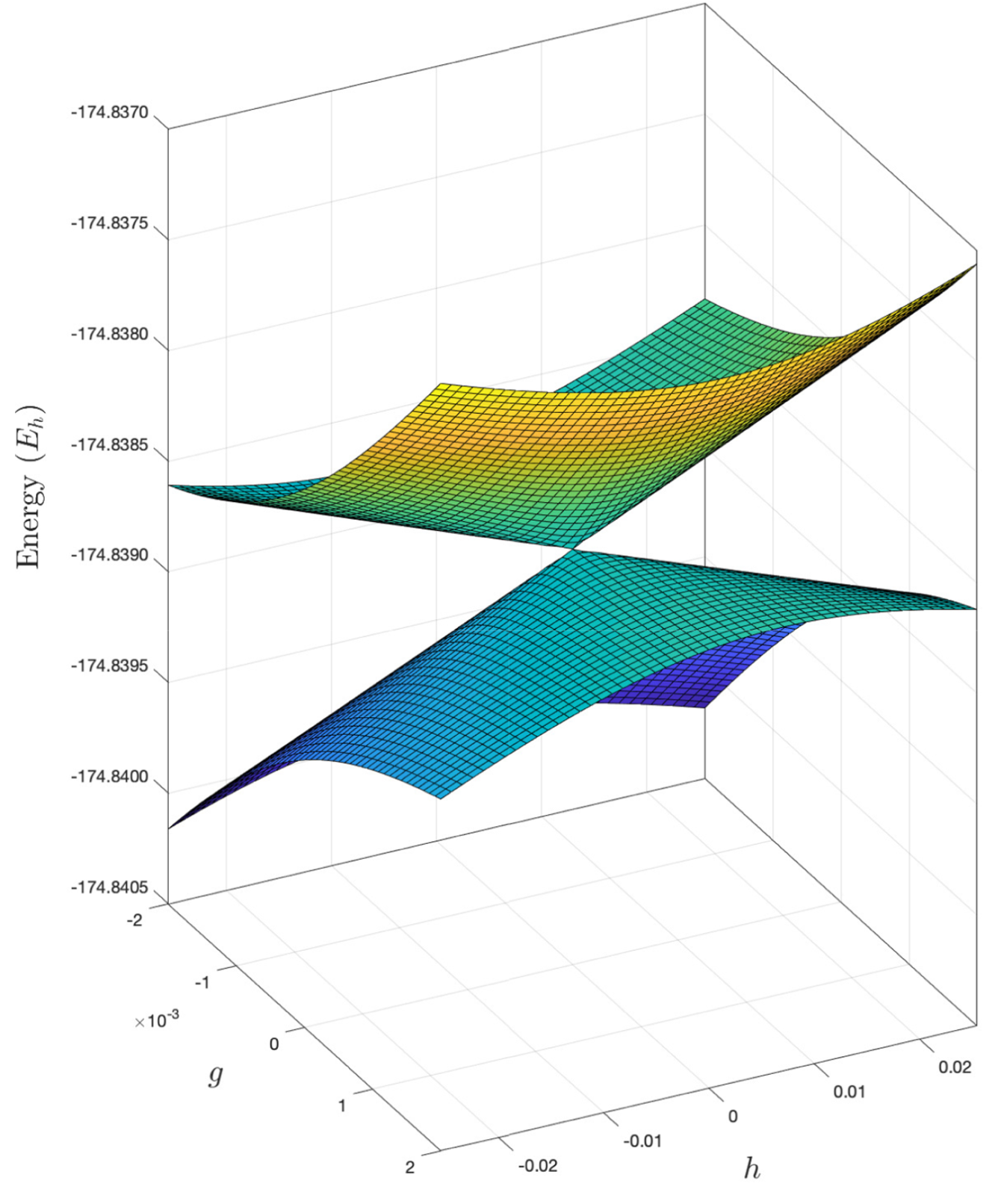
Branching or gh plane at an intersection point between the two lowest totally symmetric singlet excited states in hypofluorous acid (HOF). The energies are computed with the similarity constrained CCSD (SCCSD) and the aug-cc-pVDZ basis set [1].

Standard coupled cluster methods (CC2, CCSD, CC3, and so on) fail to correctly describe conical intersections between excited states of the same symmetry. These intersections play a central role in excited state molecular dynamics, where they mediate ultrafast internal conversion between electronic states. A physically correct description is restored in the similarity constrained coupled cluster method [1,2], which has been implemented at the singles and doubles level of theory in development versions of eT. This should make possible the use of coupled cluster theory in nonadiabatic dynamics simulations involving intersections between excited states.

References:
[1] E. F. Kjønstad and H. Koch, "An orbital invariant similarity constrained coupled cluster model", J. Chem. Theory Comput. 15(10) (2019) https://doi.org/10.1021/acs.jctc.9b00702
[2] E. F. Kjønstad and H. Koch, "Resolving the notorious case of conical intersections for coupled cluster dynamics", J. Phys. Chem. Lett. 8(19) (2017) https://doi.org/10.1021/acs.jpclett.7b02118

QED coupled cluster theory

P-nitroaniline can strongly couple to light inside an optical cavity, modifying both properties and energy levels.

In molecular polaritonics (cavity QED) we study strong interaction between light and matter, creating mixed light-matter states known as polaritons. Polaritonic states have different properties compared to pure electronic states, allowing for new and interesting chemistry. We develop methods in eT to model these light-matter systems from fundamental principles using coupled cluster theory [1]. We have demonstrated how to modify the charge transfer nature of electronic states and we have also looked into how cavities can open conical intersections.

References:
[1] T. S. Haugland, E. Ronca, E. F. Kjønstad, A. Rubio, and H. Koch "Coupled Cluster Theory for Molecular Polaritons: Changing Ground and Excited States", Phys. Rev. X 10(4) (2020) https://journals.aps.org/prx/abstract/10.1103/PhysRevX.10.041043
[2] H. Koch, "Novel wave function methods in cavity quantum chemistry", Polariton Chemistry Webinar, 25 February 2021 https://www.youtube.com/watch?v=M7FXEqFoXH0

Q-PCM-NP with QED coupled cluster theory

Ab initio plexcitons from surface plasmons in nanomaterials.

When the coupling between plasmons and molecules is sufficiently strong, the two of them combine to form plexcitons (plasmon+exciton). The characteristics of the plexciton can be found by parametrizing the plasmon as point charges (Q-PCM-NP) interacting with molecules in ab initio QED methodologies such as QED-HF and QED-CC [1]. These new plexciton states have new molecular properties arising from the strong coupling between molecules and plasmons. For instance, we observe that charge-transfer excitations splits in two (upper and lower plexciton, UP and LP) when the charge-transfer state is coupled to a resonant plasmonic-nanotip (see Figure).

References:
[1] J. Fregoni, T. S. Haugland, S. Pipolo, T. Giovannini, H. Koch* and S. Corni* "Strong Coupling between Localized Surface Plasmons and Molecules by Coupled Cluster Theory" Nano Lett. 21(15) (2021) https://doi.org/10.1021/acs.nanolett.1c02162

Molecular orbital theory in cavity QED environments

Orbital interpretation of a chemical reaction happening under strong coupling conditions in an optical cavity

Inside an optical cavity the photonic vacuum couples to molecules creating hybrid light matter states called polaritons. Since the properties of these states can be engineered tuning the photonic part of the system, polaritons have been used to modify molecular properties in a non-invasive way. Our comprehension of cavity phenomena is still limited and new insight has been gained developing a new ab-initio method that leads to the first fully consistent molecular orbital theory in the strong coupling regime. This allowed us to study a nucleophilic substitution between an ammonia molecule and a methyl chloride strongly coupled to quantum fields and to observe that the cavity induces an increase of the reaction barrier.

References:
Riso, R.R., Haugland, T.S., Ronca, E. and Koch, H. "Molecular orbital theory in cavity QED environments" Nat. Commun. 13(1) (2022) https://doi.org/10.1038/s41467-022-29003-2

Orbital localization using Edminston-Ruedenberg procedures

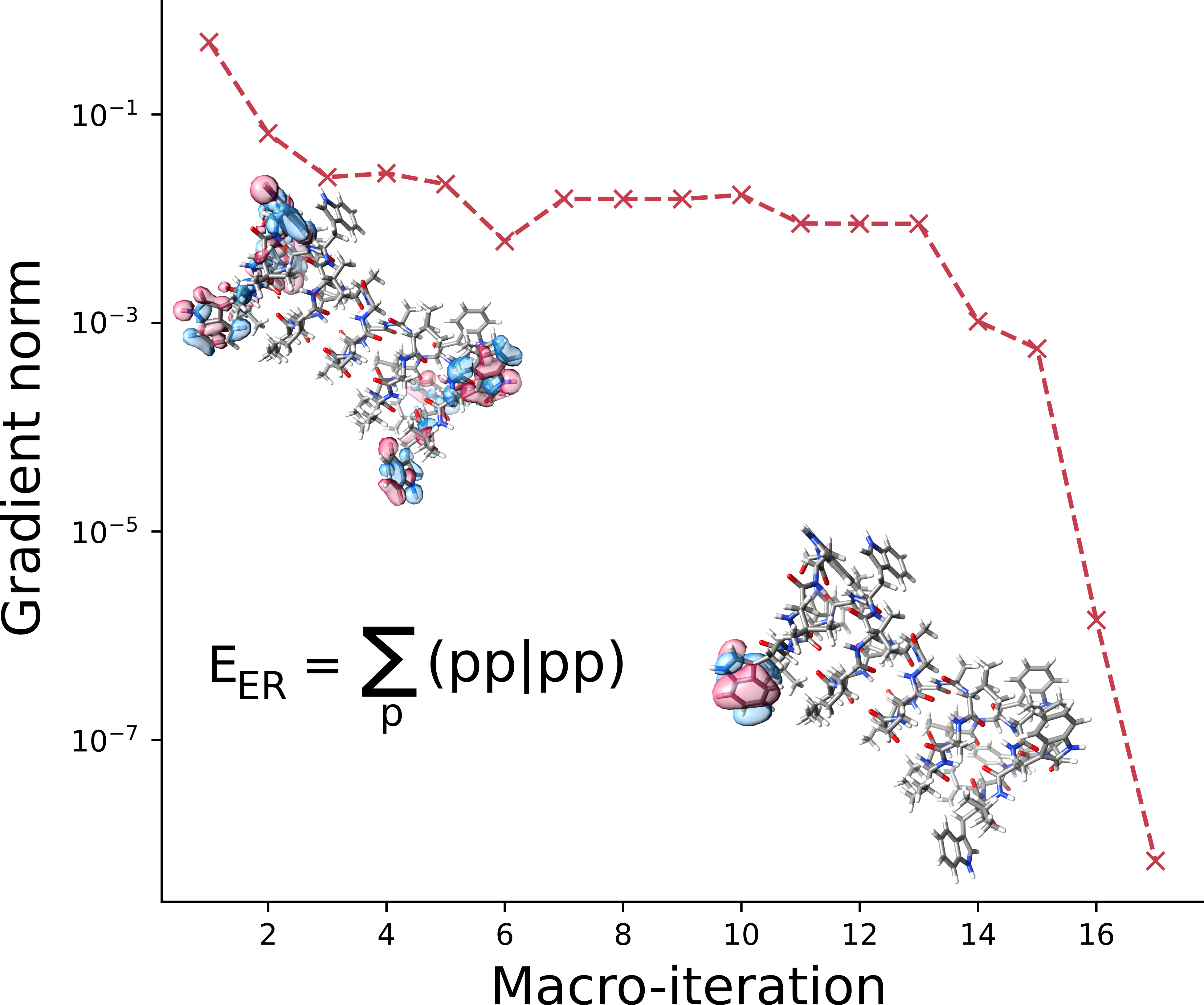
Efficient implementation of Edminston-Ruedenberg localization

In this paper, the authors describe a method for optimizing the localization of orbitals in a molecule using the Edmiston-Ruedenberg localization function. This method is used to localize both occupied and virtual orbitals, and is the first time that virtual orbital localization has been demonstrated using the Edmiston-Ruedenberg function. The optimization is performed using the molecular orbital basis and the cost of the optimization scales as O(N^4), where N is the number of basis functions. The localization of occupied orbitals is often less expensive than the corresponding self-consistent field optimization, and the cost of localizing the virtual orbitals is significantly higher. The resulting virtual orbitals have larger spreads than other, less expensive, localization functions.

References:
Sarai D. Folkestad, Regine Matveena, Ida-Marie Høyvik and Henrik Koch "Implementation of Occupied and Virtual Edmiston–Ruedenberg Orbitals Using Cholesky Decomposed Integrals" J. Chem. Theory Comput. 18(8) (2022) https://doi.org/10.1021/acs.jctc.2c00261

Resonant Inelastic X-ray Scattering within Equation-of-Motion Coupled-Cluster Damped Response (CC2, CCSD)

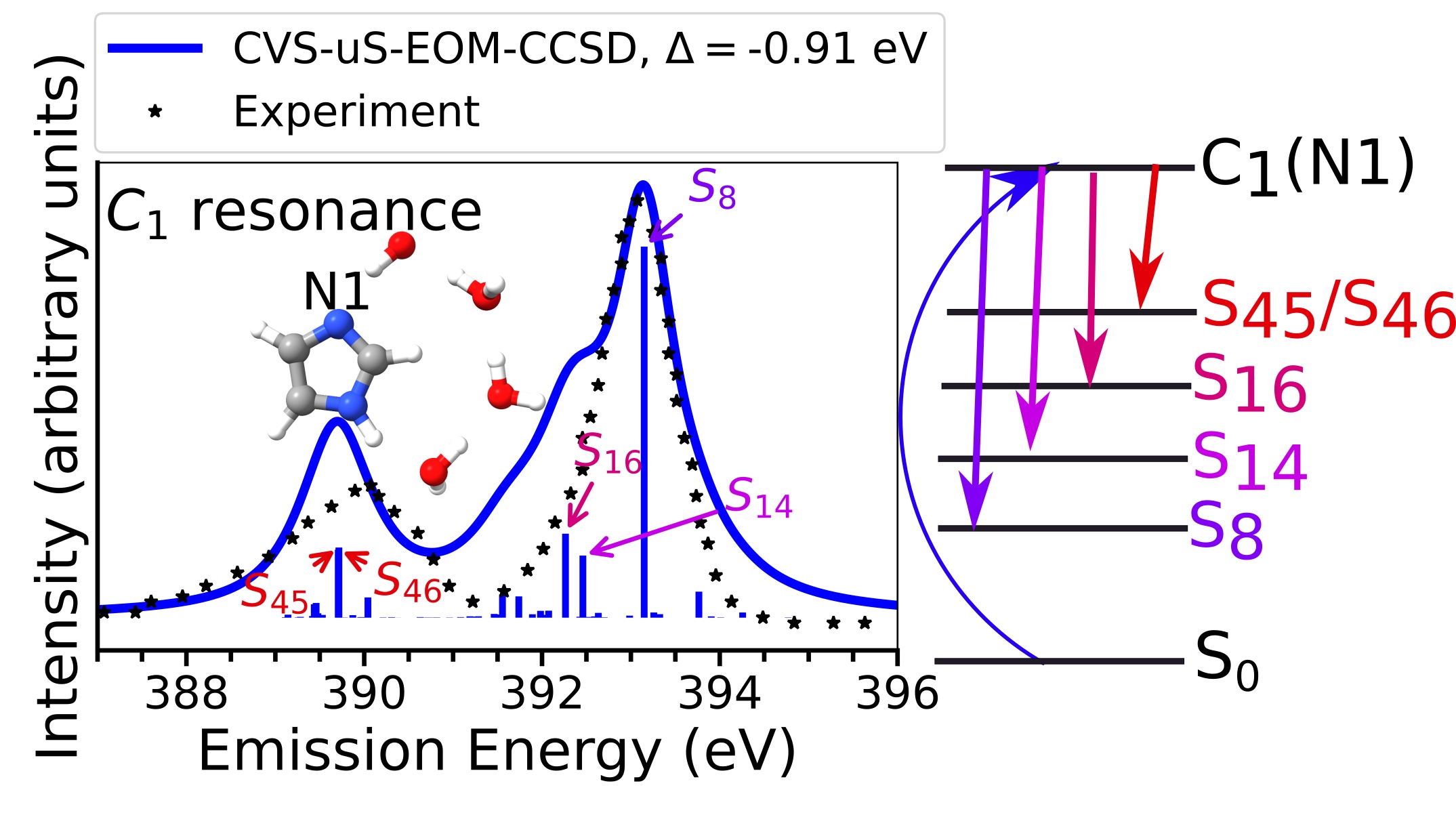
Efficient implementation of RIXS spectra

Resonant inelastic X-ray scattering (RIXS) is one of the spectroscopic techniques that has gained popularity in recent years thanks to the advances in X-ray light sources and instrumentation. With RIXS experiments becoming more feasible, the interest in theoretical approaches capable of simulating the RIXS observables has also increased, as considered essential for the interpretation of the experimental spectra. eT features an efficient implementation of the calculation of RIXS cross section [1] based on the equation of motion damped response theory framework [2] for CC2 and CCSD in gas phase and in water solution.

References:
[1] Schnack-Petersen, A. K., Moitra, T., Folkestad, S. D. and Coriani, S. "New Implementation of an Equation-of-Motion Coupled-Cluster Damped-Response Framework with Illustrative Applications to Resonant Inelastic X-ray Scattering", https://doi.org/10.48550/arXiv.2211.12215
[2] Faber, R., Coriani, S. "Resonant Inelastic X-ray Scattering and Nonesonant X-ray Emission Spectra from Coupled-Cluster (Damped) Response Theory", J. Chem. Theory Comput. 15(1) (2019) https://doi.org/10.1021/acs.jctc.8b01020